Operational Amplifiers
I. Open Loop Frequency Response (Bandwidth)
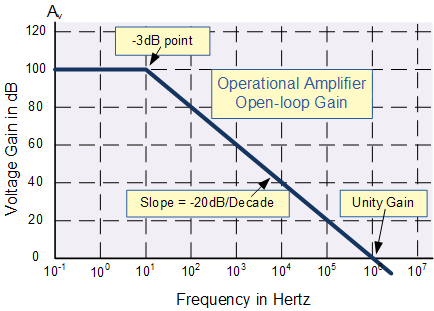
An op-amp's open-loop frequency response shows that its gain is constant and very high, then falls off at a constant rate (in dB) per frequency decade after a certain knee frequency. This knee frequency is also known as the -3dB frequency or open-loop bandwidth.
The open-loop bandwidth is the frequency at which the output signal begins to be noticeably attenuated, so it is the formal cutoff point for defining bandwidth. At this point, the output power has decreased to half of its maximum.
Decibels and Power
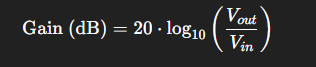
We define gain in terms of decibels to make the math easier to work with when cascading circuits with gain (decibels add instead of multiply). It's also easier to grasp since gain can range from less than 1 to millions (a very large range of numbers). Gain (dB) is calculated by:
Power in an electric circuit can simply be given by P = V2/R. So, to halve the power, the top term must be reduced to 0.5V. Since V is squared, we can do this by multiplying it by 0.707 (0.7072 = 0.5). If this were happening due to an op-amp voltage amplifier, its gain would therefore be 0.707. In dB, that's -3dB: 20 * log(0.707) = -3. This is why the open-loop bandwidth is sometimes called the -3dB frequency. In other words, the open-loop bandwidth is the frequency at which the open-loop gain decreases by -3dB.
If you know the gain in dB, the unitless (linear) gain can be calculated with anti-log:
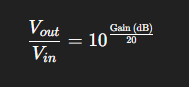
Open-Loop, Closed-Loop, Gain Bandwidth Product
The gain bandwidth product is simply the product of gain and frequency at any point on the open-loop frequency response curve after the -3dB frequency. As you can see from Figure 1, the open-loop gain in dB falls off at a constant rate of -20dB per decade after the corner frequency. This -20dB per decade is special.
Since dB represents a ratio, not a unit, the linear gain is multiplied by 0.1 every decade: 10-20/20 = 0.1 (dB adds, but linear gain multiplies. this is why we use dB in the first place. since linear gain multiplies, an addition of -20 dB is a change of x0.1, not -0.1). This change is a factor of 10 (1/10), so for every 10x increase in frequency, the gain falls off by 10x. The 10x frequency increase "cancels out" the 10x linear gain decrease when multiplied, so the product of frequency and linear gain at every point along the open-loop frequency response curve is the same.
This constant is the gain bandwidth product (GBP). The GBP is a constant for single-pole op amps because of the special -20dB per decade rolloff after the corner frequency. In the rolloff region, the product of gain and frequency is constant as previously established. In this region, Gain * frequency = constant = GBP. So, at the frequency where gain = 1 (unity gain or 0 dB), GBP = 1 * funity = funity (in other words, the numerical value of GBP is given by the unity gain frequency). The GBP in Figure 1 is 106 Hz.
By applying negative feedback (closing the loop), you're intentionally limiting the op-amp's huge open-loop gain to a precise and stable closed-loop gain, set by the feedback network. The gain is now limited by frequency as well as how much open-loop gain the op-amp has at that frequency. You're introducing the requirement that the op-amp must be able to maintain enough open-loop gain to support that closed-loop gain across the desired frequency range. Because the open-loop gain falls off with frequency, there is a point beyond which it can no longer maintain the desired closed-loop gain. This means that your desired closed-loop gain can only be supported at frequencies up to the bandwidth at that closed-loop gain. Since the GBP is constant along the curve, you can find the bandwidth for a given gain with the simple formula: Closed-loop Bandwidth = GBP / Closed-loop Gain.
Think of it this way: looking at Figure 1, if you were to configure an op amp with closed-loop negative feedback for a gain of 40 dB, the maximum frequency that it can provide that gain at is 104 Hz. Any frequency past that and the open-loop gain is falling lower than 40 dB. So, for a closed-loop gain of 40 dB in Figure 1, the bandwidth can be found by 106 / (1040/20) = 104, or 10kHz. And that equation holds true for every point along the curve: 104 * 1040/20 = 106, 105 * 1020/20 = 106, etc.